数学能力

在整个课程中，我们看到了许多不同的提示方法，可以用来提高LLM数学能力。最近的一种方法，MathPrompter，将其中一些方法（CoT，PAL等）统一到了一个技术中。总体思想是将数学问题分解为代数术语，然后使用Python代码以不同的方式解决它。

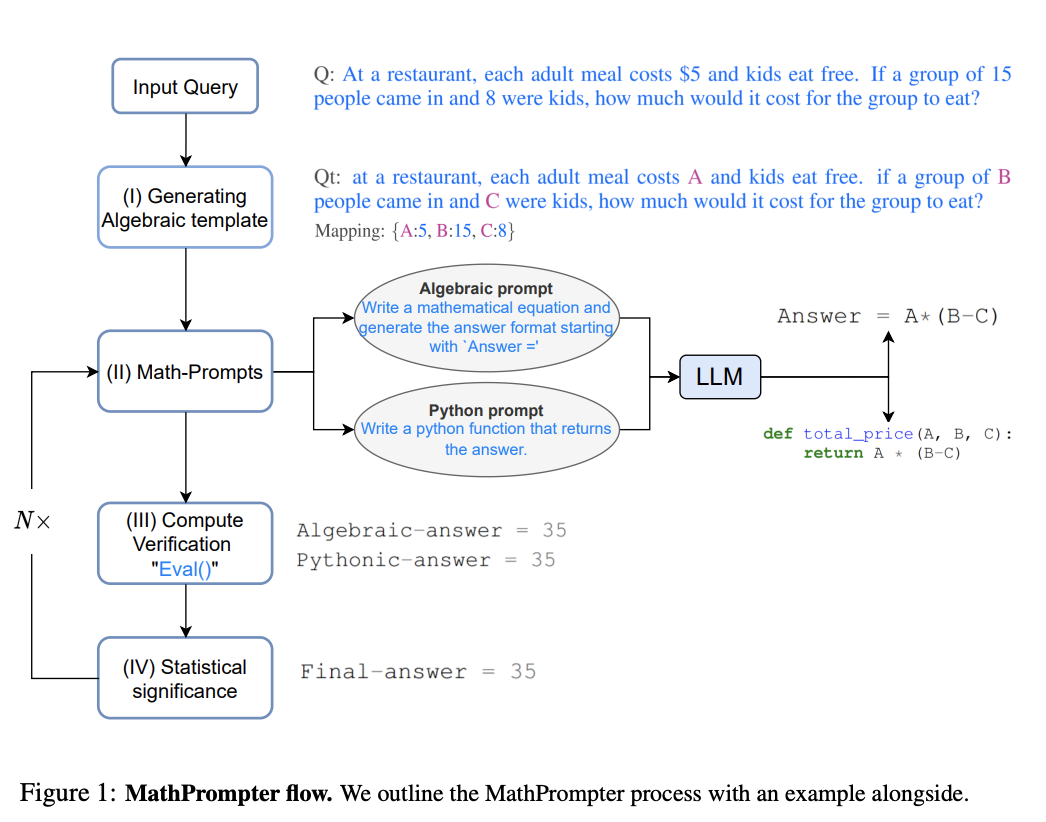
MathPrompter有四个步骤。我们将使用以下示例问题来解释它们。该示例直接取自论文。

问：在一家餐厅里，每份成人餐费用为5美元，儿童免费。如果一个由15人组成的团队进来，其中8人是儿童，那么这个团队用餐需要多少钱？

步骤1：生成代数模板

首先，我们需要为问题中的每个数字分配一个变量。这样做有助于将问题更容易地转化为一个抽象的数学问题，同时也便于编写程序代码。

这可以通过少样本提示来完成：

Q: A zoo charges $12 per adult ticket and allows children under 5 to enter for free. A family of 4 adults and 2 children under 5 visit the zoo. What is the total cost for the family to enter?

Qt: At a zoo, each adult ticket costs $A and children under 5 can enter for free. If a family of B adults and C children under 5 visit the zoo, what is the total cost for the family to enter?

Mapping: {A: 12, B: 4, C: 2}

Q: A store sells shoes at $60 per pair and socks at $8 per pair. If a customer buys 2 pairs of shoes and 3 pairs of socks, what is the total cost of the purchase?

Qt: At a store, shoes cost $A per pair and socks cost $B per pair. If a customer buys C pairs of shoes and D pairs of socks, what is the total cost of the purchase?

Mapping: {A: 60, B: 8, C: 2, D: 3}

Q: At a restaurant, each adult meal costs $5 and kids eat free. If a group of 15 people came in and 8 were kids, how much would it cost for the group to eat?

Qt: At a restaurant, each adult meal costs $A and kids eat free. If a group of B people came in and C were kids, how much would it cost for the group to eat?

Mapping:{A: 5, B: 15, C: 8}

Step 2: 第二步：数学提示

这一步的目的是将问题表述为代数表达式和Python代码。这一步有两个同时进行的提示，有助于给出问题的多样化表达。

2a: 代数表达式

我们可以使用少样本提示来让LLM将数学问题表示为代数表达式。这是通过要求LLM生成答案格式来实现的，以"Answer ="开头。

Qt: At a zoo, each adult ticket costs $A and children under 5 can enter for free. If a family of B adults and C children under 5 visit the zoo, what is the total cost for the family to enter?

Mapping: {A: 12, B: 4, C: 2}

Write a mathematical equation and generate the answer format

starting with 'Answer ='

Answer = A * B

Qt: At a store, shoes cost $A per pair and socks cost $B per pair. If a customer buys C pairs of shoes and D pairs of socks, what is the total cost of the purchase?

Mapping: {A: 60, B: 8, C: 2, D: 3}

Write a mathematical equation and generate the answer format

starting with 'Answer ='

Answer = A * C + B * D

Qt: At a restaurant, each adult meal costs $A and kids eat free. If a group of B people came in and C were kids, how much would it cost for the group to eat?

Mapping: {A: 5, B: 15, C: 8}

Write a mathematical equation and generate the answer format

starting with 'Answer ='

Answer = A * B - A * C

2b: Python 代码

我们还可以要求LLM生成解决问题的Python代码。这是通过要求LLM生成一个Python函数来实现的。

Qt: At a zoo, each adult ticket costs $A and children under 5 can enter for free. If a family of B adults and C children under 5 visit the zoo, what is the total cost for the family to enter? Mapping: `{A: 12, B: 4, C: 2}`

Write a Python function that returns the answer.

def zoo_cost(A, B, C): return A * B

Qt: At a store, shoes cost $A per pair and socks cost $B per pair. If a customer buys C pairs of shoes and D pairs of socks, what is the total cost of the purchase?

Write a Python function that returns the answer.

def store_cost(A, B, C, D): return (A * C) + (B * D)

Qt: At a restaurant, each adult meal costs $A and kids eat free. If a group of B people came in and C were kids, how much would it cost for the group to eat?

Write a Python function that returns the answer.

def restaurant_cost(A, B, C):
  return A * (B - C)

答案生成

现在，我们可以使用之前生成的映射来自动填充变量。

Mapping: {A: 5, B: 15, C: 8}

代数的：

Answer = 5 * 15 - 5 * 8

Python函数：

python

def restaurant_cost(A=5, B=15, C=8):
  return A * (B - C)

我们可以使用Python来进行评估。

代数的：:

python

>>> eval("5 * 15 - 5 * 8")
35

Python函数：

python

>>> restaurant_cost()
35

第四步：自洽性

最后，我们将利用自洽性原则多次重新运行上述过程（约5次），然后取多数答案。

结论

MathPrompter在MultiArith 数据集上报告了92.5%的准确率。这种技术的成功是一个很好的例子，展示了作为一个提示工程师，你可以将在这门课程中学到的方法结合起来，应对更大的问题。

数学能力 ​

步骤1：生成代数模板 ​

Step 2: 第二步：数学提示 ​

2a: 代数表达式 ​

2b: Python 代码 ​

答案生成 ​

第四步：自洽性 ​

结论 ​

数学能力

步骤1：生成代数模板

Step 2: 第二步：数学提示

2a: 代数表达式

2b: Python 代码

答案生成

第四步：自洽性

结论